Cell recount: People host far fewer germs
New calculations say old estimate of bacterial cells in the body was way too high
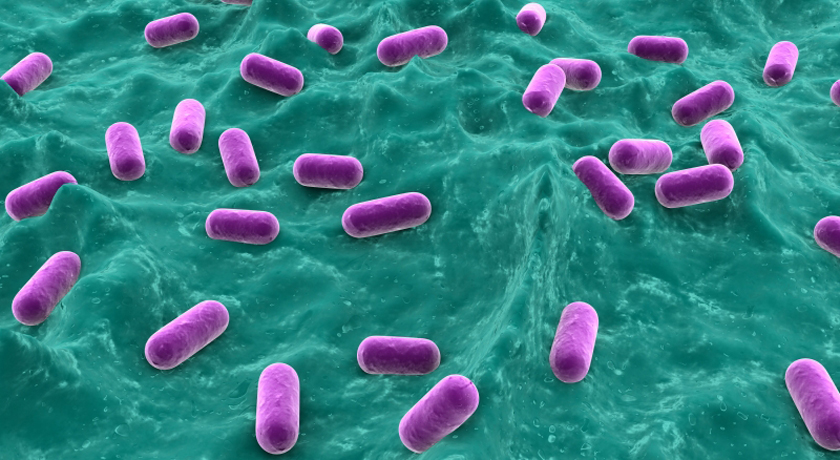
Lactobacillus bacteria, shown here colored purple (to show up against the background tissue), can live in the human gut. Some hunt down and poison disease-causing germs. That can make them quite human-friendly.
ERAXION/ ISTOCKPHOTO
For decades, scientists have been saying that our bodies are home to lots of germs. How many? About 10 bacteria for every truly human cell. But that old number, a new study finds, appears to be highly inaccurate. Humans do host lots of germs, it found — but only about 30 percent more germs than human cells, not 9,000 percent more.
Researchers shared their new calculations online January 6 at bioRxiv.org.
Scientists who study the human microbiome — that collection of microbes that call us home — have been publishing research papers repeating those old estimates of bacteria in and on the human body. They claimed that germs outnumber human cells by anywhere from 10-to-1 to 100-to-1. But in recent years, some scientists have begun to doubt those numbers.
Judah Rosner was among them. A molecular biologist, Rosner works at the National Institute of Diabetes and Digestive and Kidney Diseases in Bethesda, Md. In a 2014 issue of Microbe, he called the 10-to-1 ratio of bacteria to human cells a “fake” fact. It probably wormed its way into research papers, he says, because it sounded good. “Everybody likes a nice, round number. And it had such impact.” But Rosner and others wondered where the number had come from in the first place.
A trio of scientists took up the challenge to find out. Ron Sender and Ron Milo work at the Weizmann Institute of Science in Rehovot, Israel. Shai Fuchs had worked there with them but is now at Canada’s Hospital for Sick Children in Toronto. Together, they combed through research papers and traced the old bacterial-cell estimate to a single, “back-of-the-envelope” calculation in a 1972 paper. Then they decided to come up with their own estimates of bacterial and human-cell numbers to see how they compared.
Human cells, by percent
(story continues below image)

Red blood cells are the most common cells in the body. They account for 84 out of every 100 human cells, the team found. Then there are other cells in the blood, such as white blood cells (which fight infections) and blood-clotting cells called platelets. Altogether, 90 out of every 100 human body cells are blood cells of some type.
(Fun fact: Most human cells in the body do not contain DNA. As red blood cells mature they jettison their nuclei. These nuclei were where cells stored most of their DNA. Small structures inside cells called mitochondria (My-toh-KON-dree-uh) also have DNA. Mitochondria generate energy for cells. But red blood get rid of mitochondria, too.)
If you weigh each part of a person’s body you might think muscle and fat are the most abundant cells. They do make up 75 percent of human cells by weight. But that’s only because each is so big and heavy. In terms of numbers, muscle and fat represent only about 0.2 percent of the total. Put all the types of cells together and the body of an average man — some guy weighing 70 kilograms (154 pounds) — may be built from about 30 trillion cells, the new study finds.
As expected, most of the bacteria in the body live in the colon. This tissue, which makes up most of the large intestine, is home to an estimated 39 trillion of the 40 trillion bacterial cells in the human body.
But that bacterial estimate is not a solid number. It differs a bit, depending on who derived it, ranging anywhere from 30 trillion to 50 trillion cells. And among individual people, the new study finds, the number of resident bacteria could vary by up to 52 percent. “Indeed,” the researchers write, “the numbers are similar enough that each [poop] event may flip the ratio to favor human cells over bacteria.”
Women tend to have a smaller volume of blood than do men. That means their bacteria-to-human cell ratio may be about 30 percent higher than that of men, the researchers found. Growing children probably have a ratio of bacteria-to-human cells similar to adult men. And being fat won’t change the ratio much, the team calculates. That’s because even though people make more fat cells as they gain weight, the colon also gets bigger giving bacteria more growing room.
Still a work in progress
The new estimates by Sender, Milo and Fuchs have not been checked by other scientists yet. But already, microbiome scientists say they appreciate the team’s effort to look into the issue.
“Anytime people can add more precision, it’s good,” says Martin Blaser. He’s a microbiologist at the New York University School of Medicine. The Weizmann and Hospital for Sick Children team didn’t do any new experiments. Blaser says others should now begin measuring actual bacterial and human cell numbers to get a better gauge of the real numbers.
Other researchers also point out that the new paper’s calculations focused on bacteria. Yet the body can host other types of microbes as well. Those include viruses, fungi and archaea (Ar-KEE-uh). Viruses tend to vastly outnumber bacteria, so they could skew the microbe-to-human cell ratio upwards, says Julie Segre. A geneticist, she works at the National Human Genome Research Institute in Bethesda, Md., and is a leader of the project studying the microbiome of human skin.
Most microbiome research has focused on how the number of one type of bacteria will change when compared to another type as people get some disease. But scientists don’t yet know whether the absolute number of bacteria is also important, says Ran Blekhman. He’s a microbiologist at the University of Minnesota, in St. Paul.
Most importantly, the new estimate of how many bacteria live in and on people in no way reduces the size of the effect bacteria have on human health, scientists say. It doesn’t much matter what the real number is, most argue, as long as the number is right. Besides, “one-to-one is pretty impressive,” Rosner says. “There’s as much of them as there is of us.”
Power Words
(for more about Power Words, click here)
archaeon (plural archaea) A domain of life that includes single-celled organisms. Although archaea superficially resemble bacteria, they are distinct. Archaea inhabit many harsh environments.
back of the envelope A common phrase used to describe a calculation that is done quickly, often without much research, but just to give a preliminary estimate of some number.
colon (in biology) The majority of the large intestine, it runs between the cecum (a pouch below the small intestine) and the rectum. Foods are not digested in the colon, although this tissue lubricates wastes that will be excreted. Some liquids and salts, however, will be removed from materials stored in the colon before excretion.
fungus (plural: fungi) One of a group of single- or multiple-celled organisms that reproduce via spores and feed on living or decaying organic matter. Examples include mold, yeasts and mushrooms.
germ Any one-celled microorganism, such as a bacterium, fungal species or virus particle. Some germs cause disease. Others can promote the health of higher-order organisms, including birds and mammals. The health effects of most germs, however, remain unknown.
microbe Short for microorganism, a living thing that is too small to see with the unaided eye, including bacteria, archaea, some fungi and many other organisms such as amoebas. Most consist of a single cell.
microbiology The study of microorganisms, principally bacteria, fungi and viruses. Scientists who study microbes and the infections they can cause or ways that they can interact with their environment are known as microbiologists.
microbiota The microorganisms that live in a particular place or geological period. Scientists call the entirety of the microorganismsin a human or other animal its microbiome.
molecular biology The branch of biology that deals with the structure and function of molecules essential to life. Scientists who work in this field are called molecular biologists.
National Institute of Diabetes and Digestive and Kidney Diseases One of the 21 separate National Institutes of Health. This one both conducts internal research and finances research by others into basic biological processes and treatments for diabetes, digestive diseases and kidney diseases.
mitochondria (sing. mitochondrion) A structure in all cells (except bacteria) found outside of their nuclei. Here the cell breaks down nutrients and converts them into a form of energy known as ATP.
nucleus Plural is nuclei. (in biology) A dense structure present in many cells. Typically a single rounded structure encased within a membrane, the nucleus contains the genetic information.
platelets The smallest of blood cells, their role is to search for signs that a vessel has been damaged. Then they congregate at the site of damage and transform themselves, growing long tentacles. There they link together, creating a clot to plug any hole — stemming the potential loss of blood.
ratio The relationship between two numbers or amounts. When written out, the numbers usually are separated by a colon, such as a 50:50. That would mean that for every 50 units of one thing (on the left) there would also be 50 units of another thing (represented by the number on the right).
red blood cells Colored red by hemoglobin, these cells move oxygen from the lungs to all tissues of the body.
virus Tiny infectious particles consisting of RNA or DNA surrounded by protein. Viruses can reproduce only by injecting their genetic material into the cells of living creatures. Although scientists frequently refer to viruses as live or dead, in fact no virus is truly alive. It doesn’t eat like animals do, or make its own food the way plants do. It must hijack the cellular machinery of a living cell in order to survive.