Explainer: The basics of geometry
People have been studying geometry — points, lines, shapes, volumes — since ancient times

An up-close view of the Bent Pyramid in Dahshur, Egypt. People can learn how much rock is in this and other pyramids by using geometry.
timsdad/Wikimedia Commons
From teeny-tiny molecules in the body to jumbo jets in the air, the world is full of objects, each with its own shape. Geometry is a field of mathematics used to understand more about the lines, angles, surfaces and volumes found within our universe of objects and ideas.
And it all starts with points.
A point is a precise spot in space. Its location is so exact that it has no “size.” Instead it must be defined merely by its position.
It can be hard to picture how something could exist without having a size. So try thinking about it this way: Each point is so small that drawing a dot to mark its place would vastly cover that point and many of its neighboring points. This means that anything that can be seen or touched is made of a community of closely nested points.
The location of each point will be unique. To identify one, people have to assign it an address — one in a vast neighborhood of other points. Now consider a second point. To distinguish points, mathematicians often name them using capital letters. So we’ll call our two points A and B. We can pretend that point A lives at a make-believe address, like 123 Pointsville Road. We’ll give point B a made-up address of 130 Pointsville Road. And we can invent a name for their neighborhood, like Points’ Place.

Now draw a dot atop point A. Here, saying this dot is the same thing as a point is like saying that point A is located in the Points’ Place Neighborhood (which is true) and point A is the only thing is that neighborhood (which is false).
Drawing a dot half the size of the first one would still obscure the true point in every direction. No matter how small a dot is drawn, it will still be far bigger than the actual point. This is why mathematicians describe points as infinitely small, and therefore without size.
Even though we know that dots are too big to represent points, people still will often draw dots to represent them. Why? In such cases, the points they care about sit far enough apart that people can use tiny dots to portray the idea of them — and their relationship — in a drawing.
Lines: They aren’t just something you wait in
Lines are easier to imagine and depict. Every line is made up of points. That collection of points also is continuous. This means that each point in a line is stacked right next to two others. What’s more, there will be no empty spots between those points in a line. Even harder to picture, lines extend forever in opposite directions. Since we can’t draw something going on forever, people symbolize this idea by putting an arrow at the end of some drawing of a line. It points to the direction in which that part of the line continues.
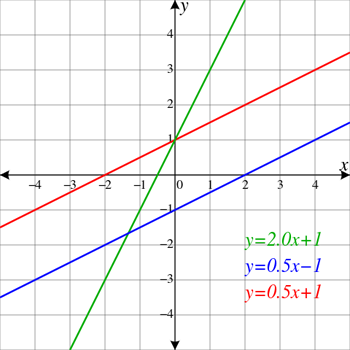
Horizontal lines extend straight from left to right, like the horizon. Slope is a term that applies to lines and surfaces. It is used to describe how steeply a line slants up or down. Lines that appear to climb upward have a positive slope. Those that seem to track downward have a negative slope. Since horizontal lines aren’t slanted at all, they have a slope of zero.
Vertical lines extend straight up and down. They are so steep that we can’t use slope as a way of describing their path. Mathematicians therefore say that the slope of these lines is undefined.
Now imagine two lines. If there’s a point at which these lines cross, that point is an intersection. Eventually, any two lines will intersect — unless they run parallel to each other. For that to be true, the lines must remain precisely the same distance from each other at every point along their paths.
A line segment is a portion of a line that has two endpoints. For instance, it can be that part of a line that runs between points A and B. A section of a line that has only one endpoint is known as a ray. A ray goes on forever in one direction.
Shapes, surfaces and solids
Our world is made from more than simple dots and lines, however. And that’s where geometry becomes especially useful. It allows people to fairly easily measure, compare and analyze shapes, especially very complex ones.
Shapes can have length and width without having depth, or thickness. When this is true, we say that a shape is two-dimensional, or 2-D. Two-dimensional shapes that have three or more straight sides are called polygons. Mathematicians name polygons by the number of sides they have. The first part of a polygon’s name is a prefix from Greek that describes how many sides it has. The second part is the suffix “-gon.” For example, penta is Greek for five. So five-sided shapes are called pentagons.
Two of the better known polygons, however, have common names that don’t follow this pattern. While we can describe three-sided shapes as trigons, nearly everyone instead calls them triangles. Similarly, four-sided ones could be tetragons, although most people actually refer to them as quadrilaterals.
In geometry, shapes and surfaces are closely related, but with important differences. Both are made up of points. However, for a shape to be a surface, the shape must be continuous. This means that there can’t be any holes or spaces between its points. If you use dashed line segments to draw a triangle on a piece of paper, that shape is not yet a surface. Go back and connect the dashed-line segments so that there are no gaps between them and now they enclose a surface.
Surfaces have length and width. However, they lack thickness. This means that anything you can touch isn’t a surface in the way that mathematicians think about them. Still, just as they use dots to represent points, we can use drawings or images to represent surfaces.
Three-dimensional (3-D) objects have length, width and depth. Such objects are also called solids. There are many examples of solids in the world around us, such as cubes, pyramids and cylinders.
Area and volume
We can measure the size of surfaces by calculating their area. Area also can be used to measure the size of objects that have thickness when we don’t need to know how thick they are. For example, by calculating the area of a floor in a house, we can figure out how much carpeting we’ll need to cover that floor. When people sell large amounts of land, sometimes they advertise that the land is a certain price per square meter (or perhaps acre).
Similarly, if we know the dimensions of a solid, geometry can let us calculate its volume. For instance, the outside dimensions of a room will tell you how much air it holds. Or the outside dimensions of a board will tell you how much wood it contains.
Mathematicians use different formulas to calculate area, based on the shape of a surface or object. For example, calculating the area of a rectangle is pretty simple. Just measure the length and the width of the rectangle, then multiply these two numbers. However, areas can quickly get more complicated to calculate when the surfaces or objects have even more sides.
If surfaces or objects are strangely-shaped, mathematicians will sometimes even calculate their area by adding together amounts for each of several sections. They get the area of each partial surface or object. Then they sum up the areas for each.
For instance, consider a piece of land where one part of it looks like a triangle and a second part looks like a square. Want to calculate the total area? Find the area of the triangular part and the area of the square part. Now add these together.
For solids, we can use a measurement called volume to describe the amount of space that a solid takes up. Mathematicians use specific formulas to calculate the volume of solids, based on the solid’s shape. Let’s say you want to find the volume of a cube. Cubes have six square sides that each have the same area. Mathematicians call each side of the cube a face. Pick any face. Now measure the length of one side of that face. Multiply this length twice by itself. For example, if the length of each side was 2 centimeters, the volume of the cube would be 2 centimeters x 2 centimeters x 2 centimeters — or 8 centimeters cubed.
These are just a few basic ideas from geometry. This field of math is so important to our understanding of the world around us that many kids take an entire class devoted to the subject in high school. People who really like the subject can study it even further by taking extra classes in high school and college. Mathematicians don’t confine their study of geometry to textbooks, however. New knowledge is emerging in this field all the time.







