For these artists, math is their muse
A growing number of artists are creating works based on mathematical ideas

"Grid," by math artist Henry Segerman, explores mathematical concepts using projections. This 3-D printed sculpture is a patterned sphere. When light shines through the openings from above, the shadows form a square grid.
H. Segerman
Every year, the Joint Mathematics Meeting brings more than 5,000 math lovers together. It’s the largest math meeting in the world. In January 2019, mathematicians flocked to the meeting in Baltimore, Md., to learn about new ideas and talk about their work. Many even — believe it or not — came to admire the latest in mathematical art.

The meeting included an entire art exhibition. Visitors marveled at sculptures made from metal, wood, porcelain and folded paper. One was based on a supersized Rubik’s cube. Many included triangles, hexagons or other shapes, arranged in strange and surprising sizes and colors. The collection also included drawings and paintings inspired by the study of numbers, curves and patterns.
Math artist Robert Fathauer, who lives near Phoenix, Ariz., organizes the art exhibit at the annual math meeting. Every year, he notes, more and more artists submit their work. Their creations explore new and creative ways to turn math into art. Fathauer himself makes pottery sculptures inspired by mathematical patterns, including those found on the frilly edges of corals or kale. He finds inspiration by looking at how math shows up in the everyday world.
“I’m always kicking around ideas in my mind,” he says.
Art and math may seem like a strange pairing. People usually experience art through their senses. They see a painting or listen to music. If this art moves them, they will have an emotional response. Solving math problems is usually viewed as something you think about — not feel.
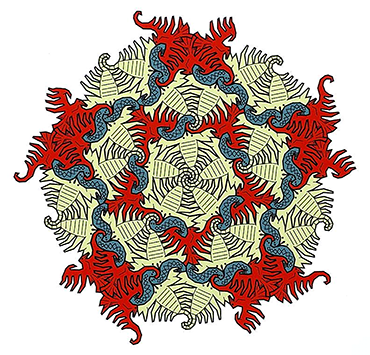
But connections between the two fields reach far back in time. Sculptors and architects in some ancient civilizations included numbers and math ideas into their works. Patterns in Islamic art that was made thousands of years ago show symmetries that mathematicians continue to study today.
“A mathematician, like a painter or a poet, is a maker of patterns,” wrote British mathematician G.H. Hardy in 1940. If a mathematician’s patterns are more permanent, he continued, “it is because they are made with ideas.”
Modern artists continue to look to math for inspiration, and in new ways. Fathauer, for instance, created a screen print inspired by his hometown. It uses three shapes — a scorpion, a snake and a bird — to cover a flat surface. The design is a nod to tessellations (Tess-uh-LAY-shuns). They are patterns that use interlocking geometric shapes to “tile,” or fill in, a two-dimensional plane. The artist lives in Phoenix (represented by a bird), where one can encounter scorpions and diamondback rattlesnakes.
The field of math art is growing. The exhibition at the 2004 Joint Mathematics Meeting, for example, included only 10 artists. By 2019, that number had grown to 94. “We get more submissions than we have room for,” Fathauer observes.

Galleries, art museums and festivals around the world have staged math art shows. In 1998, mathematicians launched the Bridges Organization, which celebrates the connections between math and art, music, architecture and culture. Every year, Bridges holds a meeting to celebrate those intersections. The Bridges conferences include art shows, talks about research on math and art, poetry readings and even performances of plays and dance inspired by art. The math art community now includes hundreds, maybe even thousands, of people around the world.
Strange shapes and four-dimensional tourists
Liz Paley is an artist in Durham, N.C. She exhibited a ceramic sculpture at the 2019 Joint Mathematics Meeting that represents a math shape known as the Klein bottle. (It’s named for the German mathematician who first described it.) This shape is special because if you trace its curves, you’ll travel over the entire surface and end up where you started. There’s no clear difference between its “inside” and “outside.” In this way, the Klein bottle only has one side.

Paley says she’s been designing Klein bottles for years. She learned about the shape almost by accident. While teaching a pottery class, a few years ago, she made a pot that she didn’t like. “One of my students asked, ‘Are you making a Klein bottle?’” Paley had never heard of it. So she began studying what makes this shape so unusual. Afterward, she started making them on purpose, experimenting with different methods and glazes. “I’ve been making them ever since,” she notes.
A Klein bottle is like a Möbius strip, which you can make by twisting a strip of paper once and then taping the ends together to make a loop. Sculpting a Klein bottle out of pottery, says Fathauer, is a tricky process: “People don’t appreciate how hard it is to do that kind of work,” he says.
Paley’s creation is about as close as we can come to a true Klein bottle. That’s because a true Klein bottle has to actually pass through itself, which is interesting to think about — but impossible to achieve in physical reality.
Her sculpture won the 2019 prize for best sculpture, textile or other material at the Joint Mathematics Meeting. She made her Klein bottle out of stoneware, the type of pottery often used to make dishes.
Math artists have used other materials for Klein bottles, as well. Bathsheba Grossman, a math sculptor who lives in Somerville, Mass., has 3-D printed her Klein bottle out of metal. She even went one step farther, adding a bottle opener to the design. So her work is a kind of math joke you can hold in your hand: It’s a Klein bottle opener.
Looking for math and finding art
Math artists tell similar stories about how they started creating. In many cases, a person who was talented in math and art had to choose one or the other as a career. But they never truly left the other behind.
Grossman went to college to study math, but while she was there she took sculpture classes. They led her to think about new ways to use 3-D printing to create shapes with surprising symmetries. Now, she’s designed hundeds of weird, geometry-inspired surfaces, and is even writing a computer program to design math sculptures.
Henry Segerman is a mathematician and artist at Oklahoma State University in Stillwater. When he was in high school, in England, he was good at math and art. But he had to choose. “I went in the math direction back then,” he says. He thought pursuing a career in art seemed “fickle” because it’s so difficult to succeed as an artist.
Still, Segerman’s math studies led him into the visual areas of math, such as geometry. “I was lucky in a way,” he says. “I was better at visualizing things than other people, and I focused on that.” But art wouldn’t leave him alone. In college and graduate school, he continued to create. Now, he creates scuptures that can cross from one dimension to another. One of his pieces, for example, is a patterned sphere. But when you shine a light from the inside out, the shadows project a square grid. This model demonstrates “projective geometry.” It’s a field of math that focuses on how different shapes and dimensions relate to one another.
In 2015, Segerman and some math art friends created a virtual-reality artwork. Participants can don a pair of VR goggles to float around and through four-dimensional shapes. Art makes it possible to interact with these shapes, which would be impossible to create in our three-dimensional world. As beautiful as it is to see, Segerman’s work also offers a new view on mathematical ideas.
Pieces of pi
Artists also find inspiration in other areas of math — including numbers themselves. John Sims is one. This math artist lives in Sarasota, Fla. His works are inspired by a combination of math, African-American culture, politics and other sources. On March 14, 2019, a gallery in Sarasota began showing some of his works inspired by the number pi.
Pi is the number found by dividing the circumference of a circle by its diameter. Because this number is the same for every circle, mathematicians call it a constant. As a decimal, pi is a number that goes on forever without repeating. Here’s how it begins, in case you want to memorize it:
The first few digits are 3.14. Sims’ art opening was chosen deliberately. March 14 is Pi Day because it’s written (in the United States, at least) as 3-14.
Since the early 2000s, Sims has organized at least 15 exhibits of math-based art. His works have been displayed in many more. He trained as a mathematician at Wesleyan University in Middletown, Conn. But when he moved to Florida, he began thinking about how to create visual versions of pi.

He began making quilts — big quilts, eight feet (2.4 meters) on a side. (He chose quilts in part because quilt-making has been an important part of the lives and history of African-Americans in the United States.) The quilts are each made of a grid of smaller squares of color. Each color corresponds to a digit. In one quilt, for example, a “3” might be represented by a black square, and “1” by green, and so on.
The center square in each quilt represents 3, the first digit in pi. Then the squares around that square line up in a color sequence that matches the next few digits of pi. And so it goes, with the colors spiraling out to the edges in a pi-inspired pattern. A viewer who doesn’t know about pi would only see a pretty color pattern. But knowing about pi helps a viewer connect art to math, Sims says.
He’s also designed quilts based on the Pythagorean (Pih-THAG-or-EE-un) theorem. To date, he has created 13 quilts. Some only use black and white. One, called “American Pi,” relies on the patriotic colors red, white and blue.
Math art, says Sims, has the ability to connect people to math in ways they hadn’t expected. Making art with pi, he says, is a natural way to do that.
“It’s part of our popular mindset,” he says.
An award-winning science writer, Stephen Ornes has been a regular contributor to Science News for Students since 2008. This piece — his 589th story for us — was inspired by his latest book: Math Art: Truth, beauty, equations (Sterling Press, New York, 2019, 192 pp).







