Math of the World
There's math in Native American beadwork, African fabrics, modern music, and even cornrow hairstyles.

There's math in the spiral pattern at the center of a flower.
Olaf Simon/iStock/Getty Images Plus
By Emily Sohn
If you know where to look, you can find math anywhere you go.
Math is not just in the numbers on a cash register or at a football game. It’s in bathroom-tiling patterns, the shapes of clouds and trees, the arrangement of a flower’s petals, a ball’s path in a pinball game, the knots you tie in your shoelaces—and even in the way you lace your shoes (see “How to Lace Like an Ace”).
Ron Eglash has gone even farther. He’s found math in beadwork, basket weaving, Navajo rugs, modern music, and even cornrow hairstyles. Eglash is a professor at Rensselaer Polytechnic Institute in Troy, N.Y.
The best way to get students excited about math, Eglash says, is to apply it to things that they care about.
With this goal in mind, he has created computer programs that reveal mathematical principles in everything from graffiti art and the architecture of African villages to Native American beadwork and Puerto Rican music. As students create and experiment, they learn math in a way that makes sense to them.
“Kids already know the mathematics, but they know it in a form that isn’t recognized in school,” Eglash says. “We’re getting kids to take something they already know in their hearts and hands and to use computers to translate that into the kind of math their schools understand.”
Fractal factor
Eglash first noticed the link between culture and math when he saw photographs of Africa taken from airplanes. Huts in many villages, he noted, are built in circles of circles of circles, or in rectangles of rectangles of rectangles.
 |
|
The walls, fences, buildings, and rooms of an African village sometimes have a pattern that repeats itself. In this illustration, notice that the smallest rectangles (blue) are miniature copies of the red rectangles, which are themselves miniature copies of the red rectangles, which are themselves miniature copies of the black rectangle. It’s possible to imagine cutting holes in the blue rectangles and adding lines to create even smaller copies of the basic rectangle design.
|
In math, a pattern that repeats itself on different scales is called a fractal. In a fractal object, each smaller structure is a miniature copy of the larger form.
Fractals often appear in nature. A tree, for instance, has branches that split into branches that split into more branches, and so on.
The rules that underlie fractals are simple. But the resulting patterns can be complex (see “Creating a Fractal Snowflake,” below).
The people who live in fractal-based villages in Africa use math to reflect spiritual concepts, Eglash says. They believe that life is a never-ending cycle and that our ancestors are always with us. Repeating patterns can also represent the desire for unending health or wealth.
 |
|
The pattern on this African (Fulani) wedding blanket has details that repeat parts of the overall design, but on smaller scales.
|
| Courtesy of Ron Eglash |
Eglash found fractals not only in village design but also in African sculptures, textiles, and other art forms.
Four points
Math and culture work together in other places, Eglash says.
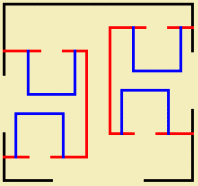
Many Native American groups, for instance, find meaning in four points that mirror each other, whether there be four directions, winds, colors, or mountains. Such four-point symmetry appears in these people’s beadwork, tepee construction, buffalo-hide drum decorations, sand paintings, and more.
 |
|
This beadwork pattern was created on a square grid.
|
| Courtesy of Ron Eglash |
In the eyes of a mathematician, these patterns belong to something called the Cartesian coordinate system. The images fit onto graphs with an x-axis and a y-axis, where each point on the graph is given by two numbers, or coordinates. And there are sets of rules, called algorithms, that tell you how draw these shapes step by step on graph paper (or a computer screen).
Using Eglash’s Virtual Bead Loom program, you can experiment with the Cartesian coordinate system to make your own beautiful works of art. You can also try the Graffiti Grapher, Navajo Rug Weaver, and Alaskan Basket Weaver, all based on the same concept.
Drumbeats and cornrows
Among Eglash’s other creations is a program called Rhythm Wheels. It challenges kids to figure out when two repeating sets of drumbeats, each going at its own pace, will meet. As they work with this program, kids learn about fractions and finding the least common denominator.
Cornrow Curves, another program, teaches transformational geometry. Students work with repeating patterns and changes in scale to create new hairstyles.
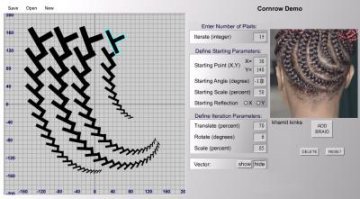 |
|
Ron Eglash’s software can be used to create cornrow hairstyle designs.
|
| Rensselaer/Eglash |
Eglash can’t look anywhere without seeing a math lesson just waiting to be taught. His newest program, still under construction, uses a break-dancing robot to explain angles involved in three-dimensional movement around an axis.
Eglash’s math programs are popular with students. According to recent studies, a group of mostly minority kids felt better about computers after using them. And a group of mostly Latin American students improved their math grades after using the tools.
Math appreciation
In Native American communities, elders appreciate the lessons, too, because kids learn about the history of their people.
In fact, each of Eglash’s programs includes information about the culture, history, and math involved.
 |
|
With Eglash’s computer program, it’s possible to create a weaving pattern (right) that looks like the one used to make a real basket (left).
|
| Courtesy of Ron Eglash |
Once parents and grandparents consider schoolwork to be culturally valuable, they become more likely to encourage their kids to study, says Jim Barta. He’s a professor at Utah State University in Logan.
“Parents say, ‘Wow, I wish I’d had teachers that taught me math that way. I might have liked it!'” Barta says.
Ultimately, mixing math with culture could do more than help kids learn. It could also help them understand each other better.
“Culture is usually a barrier to math,” Eglash says. “We are using math as a bridge to culture.”
Creating a Fractal Snowflake
You will need:
- pencil
- ruler
- sheet of paper
- protractor for measuring angles to draw triangles
 |
What to do:
- Draw an equilateral triangle with each side measuring 9 centimeters (above left). (Remember, each angle of an equilateral triangle measures 60°.
- Divide each 9-centimeter side into three equal parts, each measuring 3 centimeters. At the middle of each side, add an equilateral triangle one-third the size of the original, facing outward. Because each side of the original triangle 9 centimeters, the new, smaller triangles will have 3-centimeter sides. When you examine the outer edge of your diagram, you should see a six-pointed star made up of 12 line segments (above middle).
- At the middle of each segment of the star, add a triangle one-ninth the size of the original triangle. The new triangle will have sides 1 centimeter in length, so divide each 3-centimeter segment into thirds, and use the middle third to form a new triangle (above right).
- Going one set further, you create a shape that begins to resemble a snowflake (below).
 |
If you were to continue the process by endlessly adding smaller and smaller triangles to every new side, you would produce a fractal object that mathematicians call the von Koch snowflake curve, named after a Swedish mathematician, Niels Fabian Helge von Koch.
 |
Going Deeper:







