The five-second rule: Myth busted?
After the bologna drops and the microbes grow, it’s time to look at the unappetizing results

Is this bologna bacteria-free? An experiment should answer that question. Now it’s time to analyze the data.
Explainr
This article is one of a series of Experiments meant to teach students about how science is done, from generating a hypothesis to designing an experiment to analyzing the results with statistics. You can repeat the steps here and compare your results — or use this as inspiration to design your own experiment.
Many of us have dropped food on the floor — then picked it up and eaten it. Some people even say that if the food has been on the floor for less than five seconds, it’s probably still clean. But does time even matter? The latest DIY Science video tests whether that “five-second rule” is true. The results show that bacteria are everywhere, and they are not waiting before hopping onto your food.
In fact, our bologna grew plenty of bacteria, even if it wasn’t dropped at all. Five seconds, 50 seconds or zero seconds made no difference.
In the first blog post, we came up with a hypothesis to test: that food picked up off the floor after five seconds will collect fewer bacteria than food left on the floor for 50 seconds. To test this hypothesis, we dropped bologna. Then we figured out how to measure how dirty or clean the bologna was by growing bacteria in petri dishes. We needed six groups of dishes. (One was a control. One grew microbes from bologna that had never been dropped. The other four hosted bacteria swabbed from bologna that sat for five or 50 seconds each on sections of clean and dirty floor.)
Our second blog post described how I performed the experiment, from dropping the bologna to growing any microbes that were on the food. After each drop, I swabbed the meat carefully and rubbed the swab on a petri dish containing agar — a gel-like substance bacteria like to munch on. The plates then sat for three days in a homemade incubator, which kept them warm.
Counting colonies
On each of those three days, I photographed each plate with a smartphone. I made sure the light was the same for all my images, and I took my pictures at the same time every day. I uploaded the pictures to a computer and used a program — ImageJ — to count how many colonies of microbes grew. ImageJ is available to download free from the National Institutes of Health. It’s used to analyze science images. Details on how to use the program to count colonies can be found in this tutorial.
Since I had 36 plates and photographed each of them three times, I had to run the ImageJ analysis 108 times! After each run, I noted the number of colonies. (I used a computer spreadsheet, Microsoft Excel, but other programs, such as Google Sheets, will also work. My full data tables are at the bottom of this post.)
Then, for each group and each day, I calculated the mean — or average — number of microbial colonies. To find that number, I added the colonies from all six petri dishes from a single test condition and divided the result by six (which is the number of plates per group). I also calculated the standard error of the mean. That’s how much the numbers of colonies might vary in general, based on the plates sampled. (For more on how to calculate this number, read this blog post.)
Once I had calculated all the means and standard errors, I graphed the results using a free trial of the program GraphPad Prism.
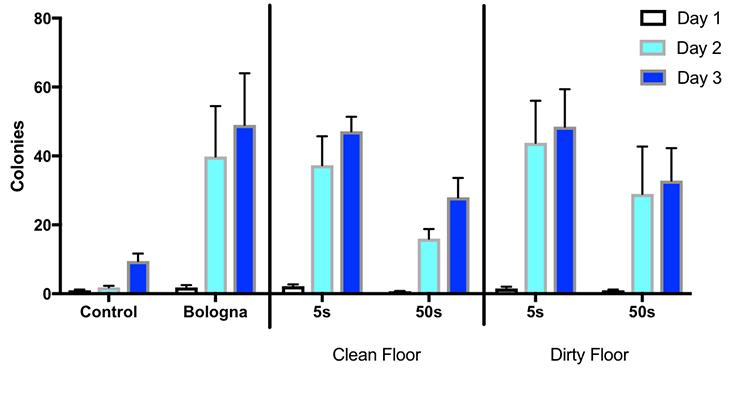
In the chart, each grouping of three bars represents the colonies counted on the dishes over three days. The groupings are labeled along the bottom, on the x axis. The vertical, or y axis, marks the number of microbial colonies that grew on the plates. The bars on far left represent the control; it had no bologna, just agar and distilled water. To its right is bologna that was never dropped. The two middle groups are bologna dropped on a clean floor and left for five and 50 seconds. The two groups on the right are bologna dropped on a dirty floor and left for five and 50 seconds.
The results show that the microbes needed a little time to grow into bunches big enough to see. On the first day, most of the plates had very few colonies. But by the second and third days, the dishes that had been smeared with eau de bologna sprouted plenty of bacterial colonies. A few microbes even grew on the clean plates swabbed only with distilled water.
From the graph above, it looks like bologna alone grew lots of bacteria. And picking the food up after five seconds appears to have not protected it from microbes. But we can’t make conclusions about the experiment just by looking at the results. We need to use statistics to analyze the data and find out what it all means.
Our hypothesis is that the amount of time on the floor matters: Food picked up after five seconds will have fewer microbial colonies than food picked up after 50 seconds. To test that, we need to compare all six groups at the same time. We’ll analyze the data from day three only.
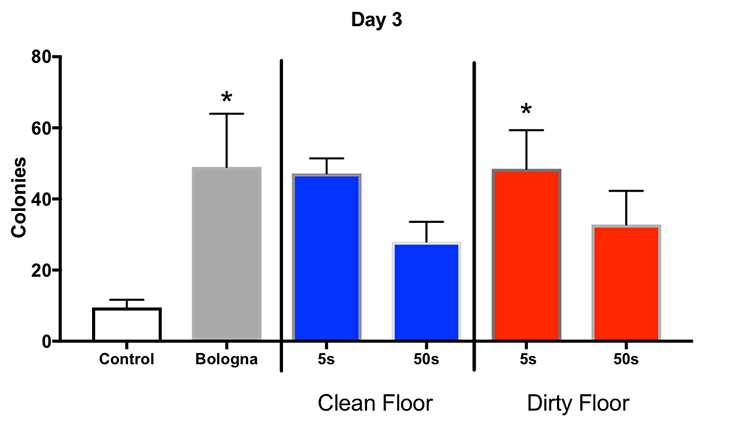
By day three, the control, on average, grew about nine colonies per plate. In contrast, all the bologna plates grew an average of more than 20 colonies each. Some grew almost 50. (Ewwwww!)
The little Ts sticking out of the bars represent the standard error of the mean. That is how much the data spread. In many of the groups, the data spread a lot. That can make it difficult to tell if there is truly a difference between the groups.
A statistical test called an analysis of variance, or ANOVA, can help here. It’s a test used to compare two or more groups. (For more on ANOVAs, check out this blog post.) GraphPad can calculate the ANOVA. For this data, it generates a table that looks like this:
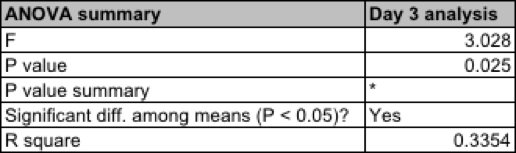
An ANOVA compares results from one group to those from the other groups. The most important number is the p value (0.025). The p value is the probability of seeing a difference in the number of colonies as large or larger than the one found in my experiment — if there was no actual difference between the groups, and the result happened only by accident. Many scientists accept a p value of 0.05 (five percent) or less to be statistically significant — unlikely to be due to chance. Our p value is less than 0.05. This suggests differences this big would occur only about five percent of the time if the difference wasn’t really there.
But the ANOVA only gives results overall. It says each of the groups are different from each other but not whether there was a difference between the two time periods, five and 50 seconds. A post-hoc test will determine if there are additional differences in the data. GraphPad can calculate this.
The results of the post-hoc test are marked as stars on the graph. Each star represents a p value of less than 0.05 compared to the control. The bologna left on the dirty floor for five seconds had significantly more microbes on it than the control. But so did bologna that was never dropped at all!
What can we conclude? Microbes show up, whether or not food has touched the floor. And time doesn’t matter when it comes to keeping bologna clean.
Any bacteria on that food probably wouldn’t make you sick, fortunately. Our guts are very good at fighting off most germs.
So, can we declare this myth busted? The next post will discuss the limitations of the experiment, and talk about other studies that have taken on the five-second rule.
Explainr