Explainer: All about orbits
An orbit is the route that one space object repeatedly takes around another

Comets — such as Neowise C/2020 F3, seen here — travel around the sun in very elliptical orbits.
Anton Petrus/Moment/Getty Images Plus
By Trisha Muro
Even in ancient times, stargazers knew that planets differed from stars. While stars always appeared in the same general place in the night sky, planets shifted their positions from night to night. They appeared to move across the backdrop of stars. Sometimes, planets even appeared to move backward. (This behavior is known as retrograde motion.) Such strange movements across the sky were hard to explain.
Then, in the 1600s, Johannes Kepler identified mathematical patterns in the planets’ movements. Astronomers before him had known that the planets orbited, or moved around the sun. But Kepler was the first to describe those orbits — correctly — with math. As if putting together a jigsaw puzzle, Kepler saw how the pieces of data fit together. He summed up the math of orbital motion with three laws:
- The path a planet takes around the sun is an ellipse, not a circle. An ellipse is an oval shape. This means that sometimes a planet is closer to the sun than at other times.
- A planet’s speed changes as it moves along this path. The planet speeds up when passing closest to the sun and slows as it gets farther away from the sun.
- Each planet orbits the sun at a different speed. The more distant ones move more slowly than those closer to the star.
Kepler still couldn’t explain why planets follow elliptical paths and not circular ones. But his laws could predict planets’ positions with incredible accuracy. Then, about 50 years later, physicist Isaac Newton explained the mechanism for why Kepler’s laws worked: gravity. The force of gravity attracts objects in space to each other — causing the motion of one object to continually bend toward another.
Throughout the cosmos, all sorts of celestial objects orbit each other. Moons and spacecraft orbit planets. Comets and asteroids orbit the sun — even other planets. Our sun orbits the center of our galaxy, the Milky Way. Galaxies orbit each other, too. Kepler’s laws describing orbits hold true for all these objects across the universe.
Let’s have a look at each of Kepler’s laws in more detail.
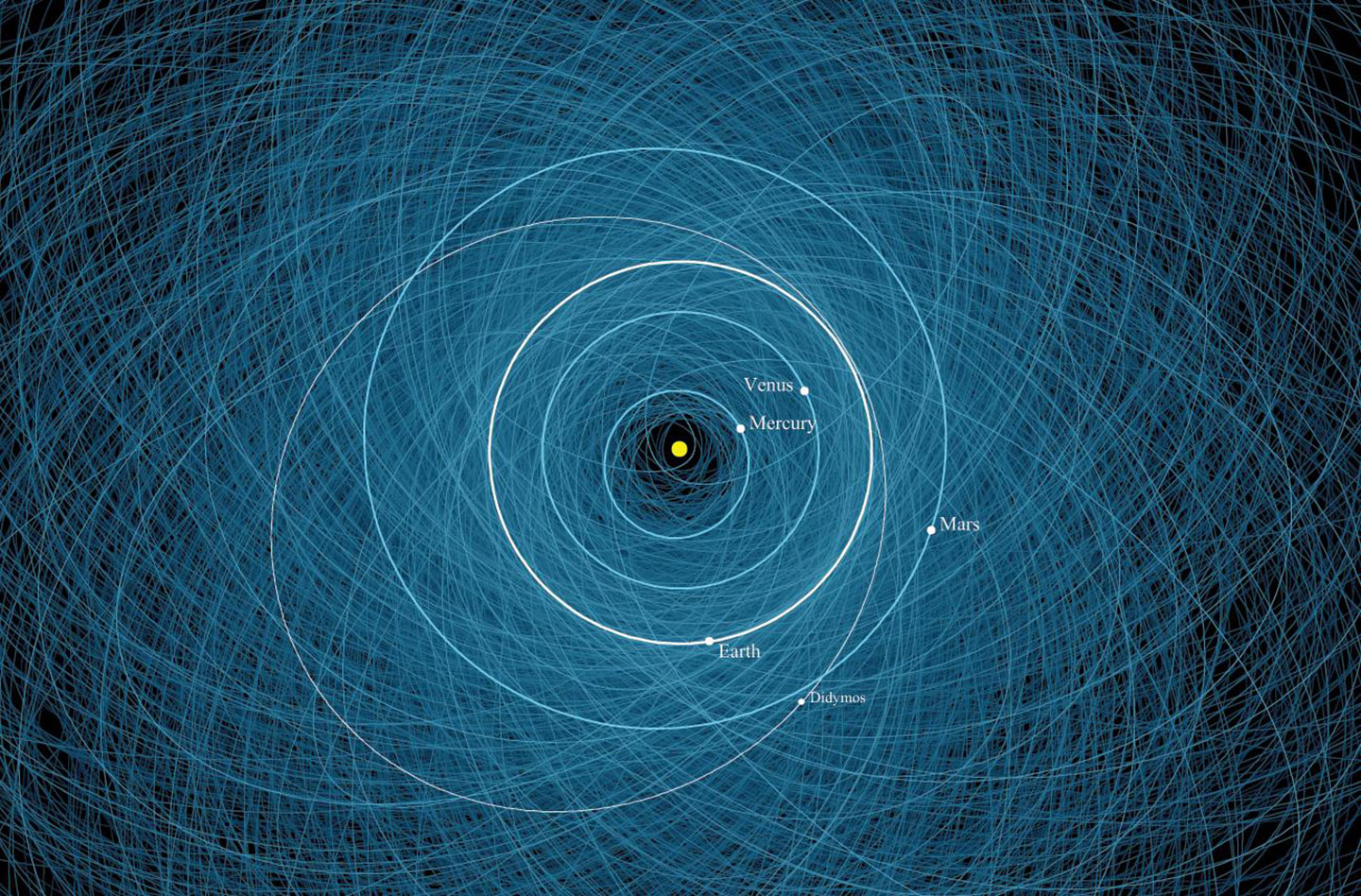
Kepler’s First Law: Ellipses
To describe how oval-like an ellipse is, scientists use the word eccentricity (Ek-sen-TRIS-sih-tee). That eccentricity is a number between 0 and 1. A perfect circle has an eccentricity of 0. Orbits with eccentricities closer to 1 are really stretched-out ovals.
The moon’s orbit around Earth has an eccentricity of 0.055. That’s almost a perfect circle. Comets have very eccentric orbits. Halley’s Comet, which whizzes by Earth every 75 years, has an orbital eccentricity of 0.967.
(It is possible for an object’s motion to have an eccentricity greater than 1. But such a high eccentricity describes an object whipping around another in a wide U-shape — never to return. So, strictly speaking, it would not be orbiting the object its path was bent around.)
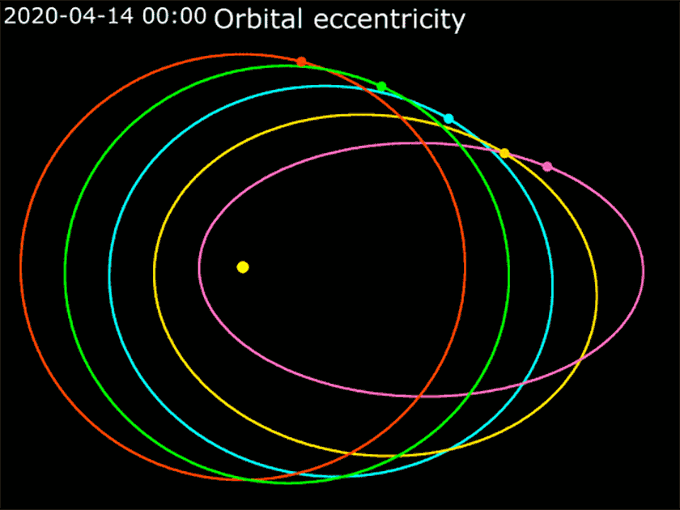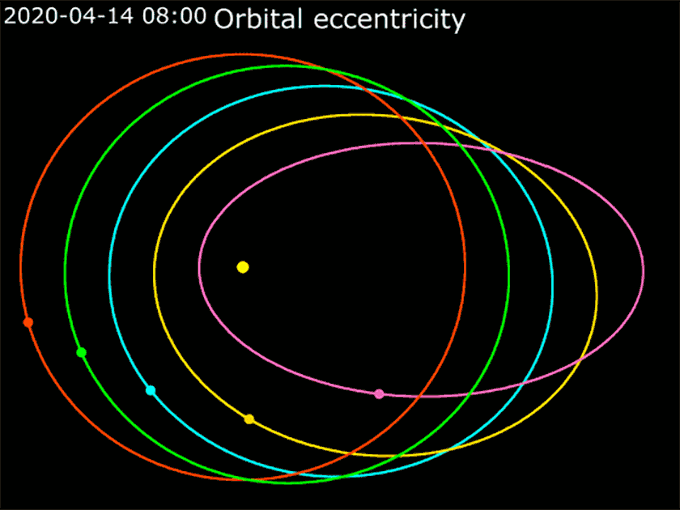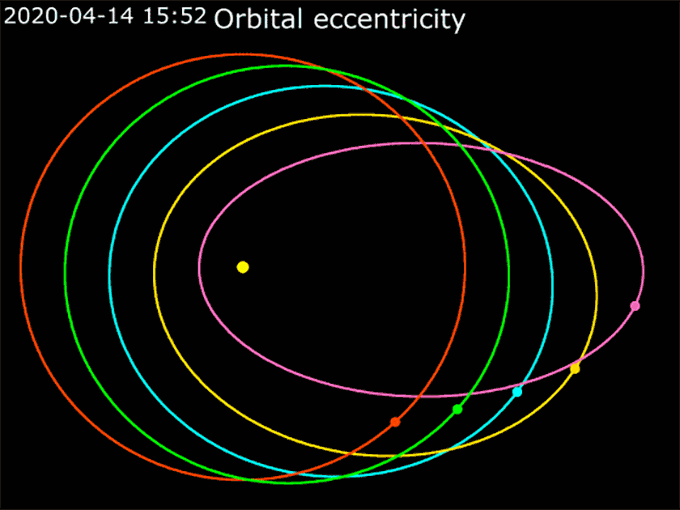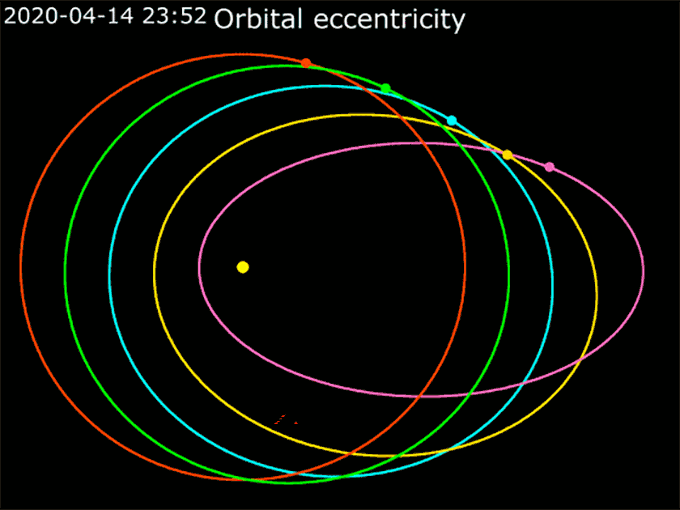
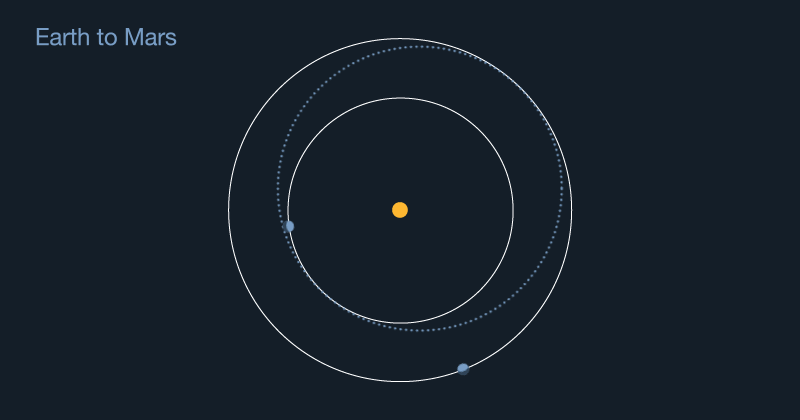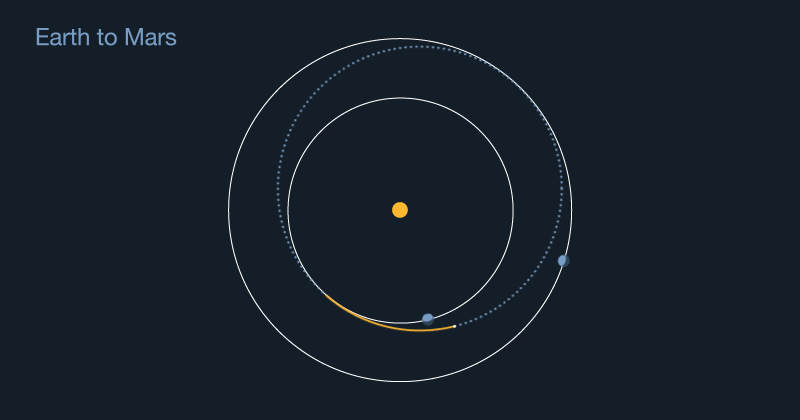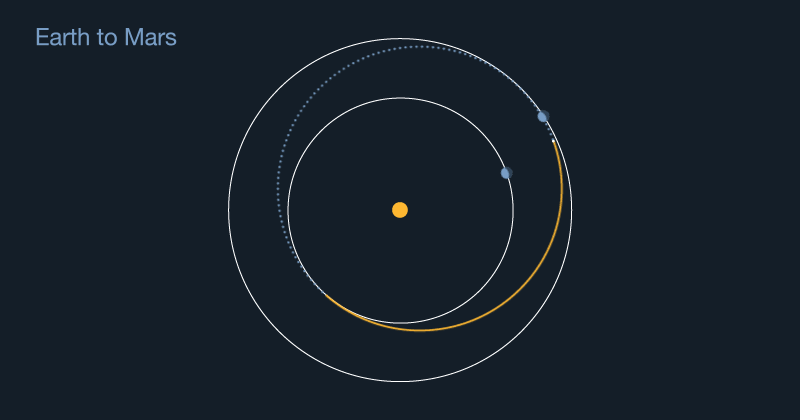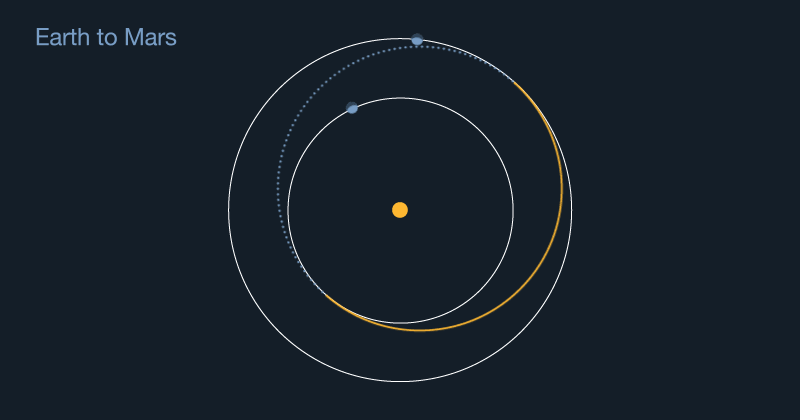
Ellipses are very important for planning a spacecraft’s orbit. If you want to send a spacecraft to Mars, you have to remember that the spacecraft starts from Earth. That might sound silly at first. But when you launch a rocket, it will naturally follow the ellipse of Earth’s orbit around the sun. To reach Mars, the spacecraft’s elliptical path around the sun will have to change to match Mars’ orbit.
With some very complex math — that famous “rocket science” — scientists can plan how fast and how high a rocket needs to launch a spacecraft. Once the spacecraft is in orbit around Earth, a separate set of smaller engines slowly widens the craft’s orbit around the sun. With careful planning, the spacecraft’s new orbital ellipse will exactly match Mars’ at just the right time. That allows the spacecraft to arrive at the Red Planet.
Kepler’s Second Law: Changing speeds
The point where a planet’s orbit comes closest to the sun is its perihelion. The term comes from the Greek peri, or near, and helios, or sun.
Earth reaches its perihelion in early January. (This may seem strange to people in the Northern Hemisphere, who experience winter in January. But Earth’s distance from the sun is not the cause of our seasons. That’s due to the tilt of Earth’s axis of rotation.) At perihelion, Earth is moving fastest in its orbit, about 30 kilometers (19 miles) per second. By early July, Earth’s orbit is at its farthest point from the sun. Then, Earth is traveling most slowly along its orbital path — about 29 kilometers (18 miles) per second.
Planets are not the only orbiting objects that speed up and slow down like this. Whenever something in orbit gets closer to the object it’s orbiting, it feels a stronger gravitational pull. As a result, it speeds up.
Scientists try to use this extra boost when launching spacecraft to other planets. For instance, a probe sent to Jupiter might fly past Mars on the way. As the spacecraft gets closer to Mars, the planet’s gravity causes the probe to speed up. That gravitational boost flings the spacecraft toward Jupiter much faster than it would travel on its own. This is called the slingshot effect. Using it can save a lot of fuel. Gravity does some of the work, so the engines need to do less.
Educators and Parents, Sign Up for The Cheat Sheet
Weekly updates to help you use Science News Explores in the learning environment
Thank you for signing up!
There was a problem signing you up.
Kepler’s Third Law: Distance and Speed
At an average distance of 4.5 billion kilometers (2.8 billion miles), the sun’s gravitational pull on Neptune is strong enough to hold the planet in orbit. But it’s much weaker than the sun’s tug on Earth, which is a mere 150 million kilometers (93 million miles) from the sun. So, Neptune travels along its orbit more slowly than Earth does. It cruises around the sun at about 5 kilometers (3 miles) per second. Earth zooms around the sun at about 30 kilometers (19 miles) per second.
Since more distant planets travel more slowly around wider orbits, they take much longer to complete one orbit. This time span is known as a year. On Neptune, it lasts about 60,000 Earth days. On Earth, far closer to the sun, a year is just a bit more than 365 days long. And Mercury, the planet closest to the sun, wraps up its own year every 88 Earth days.
This relationship between an orbiting object’s distance and its speed affects how fast satellites zoom around Earth. Most satellites — including the International Space Station — orbit about 300 to 800 kilometers (200 to 500 miles) above Earth’s surface. Those low-flying satellites complete one orbit every 90 minutes or so.
Some very high orbits — around 35,000 kilometers (20,000 miles) off the ground — cause satellites to move more slowly. In fact, those satellites move slowly enough to match the speed of Earth’s rotation. These craft are in geosynchronous (Gee-oh-SIN-kron-ous) orbit. Since they seem to stand still above a single country or region, these satellites are often used to track weather or relay communications.
On collisions and ‘parking’ spots
Space may be huge, but everything in it is always in motion. Occasionally, two orbits cross one another. And that can lead to collisions.
Some places are packed with objects on crisscrossing orbits. Consider all of the space junk orbiting Earth. These bits of debris are constantly colliding with each other — and occasionally with important spacecraft. Predicting where potentially hazardous pieces of debris are headed in this swarm can be quite complex. But it’s worth it, if scientists can foresee a collision and move a spacecraft out of the way.
Sometimes, the target of a potential collision may not be able to divert its path. Consider a meteor or other space rock whose orbit may put it on a collision course with Earth. If we’re lucky, that incoming rock will burn up in Earth’s atmosphere. But if the boulder is too big to fully disintegrate on its way through the air, it could smash into Earth. And that could prove disastrous — just as it was for the dinosaurs 66 million years ago. To head off these problems, scientists are investigating how to divert the orbit of the incoming space rocks. That takes an especially challenging number of orbital calculations.
Saving satellites — and potentially warding off the apocalypse — are not the only reasons to understand orbits.
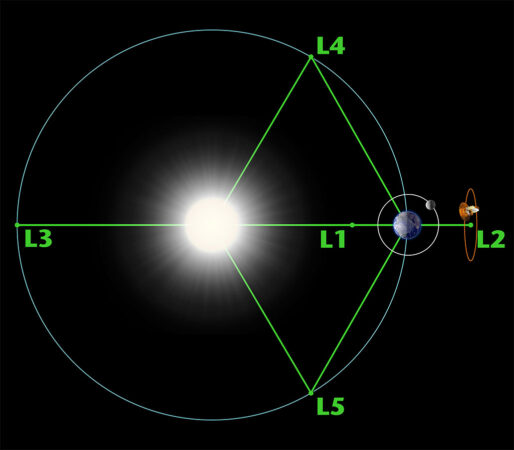
In the 1700s, mathematician Joseph-Louis Lagrange identified a special set of points in space around the sun and any given planet. At these points, the gravitational pull of the sun and the planet strike a balance. As a result, a spacecraft parked in that spot can stay there without burning much fuel. Today, these are known as Lagrange points.
One of those points, known as L2, is especially useful for space telescopes that need to stay very cold. The new James Webb Space Telescope, or JWST, takes advantage of that.
Orbiting at L2, JWST can point away from both the Earth and sun. This allows the telescope to make observations anywhere in space. And since L2 is about 1.5 million kilometers (1 million miles) away from Earth, it is far enough from both the Earth and the sun to keep JWST’s instruments extremely cool. But L2 also allows JWST to stay in constant communication with the ground. As JWST orbits the sun at L2, it will always be the same distance from Earth — so the telescope can send its stunning views home while facing out into the universe.







