(for more about Power Words, click here)
computer model A program that runs on a computer that creates a model, or simulation, of a real-world feature, phenomenon or event.
confounding (in statistics) A situation where one or more unrecognized variables (conditions or events) were responsible for some effect. This could give the faulty impression that the effect was due to something else. Confounding often occurs when researchers did not “control” for the possibility that other variables were or could be at work.
control A part of an experiment where there is no change from normal conditions. The control is essential to scientific experiments. It shows that any new effect is likely due only to the part of the test that a researcher has altered. For example, if scientists were testing different types of fertilizer in a garden, they would want one section of it to remain unfertilized, as the control. Its area would show how plants in this garden grow under normal conditions. And that give scientists something against which they can compare their experimental data.
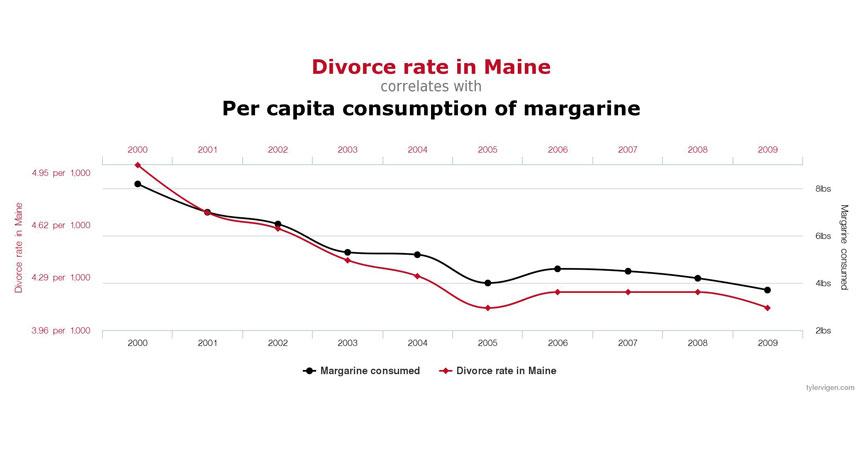
correlation A mutual relationship or connection between two variables. When there is a positive correlation, an increase in one variable is associated with an increase in the other. (For instance, scientists might correlate an increase in time spent watching TV with an increase in risk of obesity.) Where there is an inverse correlation, an increase in one value is associated with a decrease in the other. (Scientists might correlate an increase in TV watching with a decrease in time spent exercising each week.) A correlation between two variables does not necessarily mean one is causing the other.
data Facts and statistics collected together for analysis but not necessarily organized in a way that give them meaning. For digital information (the type stored by computers), those data typically are numbers stored in a binary code, portrayed as strings of zeros and ones.
doctoral degree Also known as a PhD or doctorate, these are advanced degrees offered by universities — typically after five or six years of study — for work that creates new knowledge. People qualify to begin this type of graduate study only after having first completed a college degree (a program that typically takes four years of study).
engineer A person who uses science to solve problems. As a verb, to engineer means to design a device, material or process that will solve some problem or unmet need.
engineering The field of research that uses math and science to solve practical problems.
ethics (adj. ethical) A code of conduct for how people interact with others and their environment. To be ethical, people should treat others fairly, avoid cheating or dishonesty in any form and avoid taking or using more than their fair share of resources (which means, to avoid greed). Ethical behavior also would not put others at risk without alerting people to the dangers beforehand and having them choose to accept the potential risks.
factor Something that plays a role in a particular condition or event; a contributor.
lead A toxic heavy metal (abbreviated as Pb) that in the body moves to where calcium wants to go. The metal is particularly toxic to the brain, where in a child’s developing brain it can permanently impair IQ, even at relatively low levels.
model A simulation of a real-world event (usually using a computer) that has been developed to predict one or more likely outcomes.
statistical analysis A mathematical process that allows scientists to draw conclusions from a set of data. In research, a result is significant (from a statistical point of view) if the observed difference between two or more conditions is unlikely to be due to chance. Obtaining a result that is statistically significant means that it is unlikely to observe that much of a difference if there really is no effect of the conditions being measured.
statistical significance In research, a result that appears reliable — or significant — from a mathematical point of view. Findings that are statistically significant have a reduced likelihood that the apparent link between two or more conditions is a fluke, or merely due to chance.
statistics The practice or science of collecting and analyzing numerical data in large quantities and interpreting their meaning. Much of this work involves reducing errors that might be attributable to random variation. A professional who works in this field is called a statistician.
variable (in mathematics) A letter used in a mathematical expression that may take on different values. (in experiments) A factor that can be changed, especially one allowed to change in a scientific experiment. For instance, when researchers measure how much insecticide it might take to kill a fly, they might change the dose or the age at which the insect is exposed. Both the dose and age would be variables in this experiment.