Pesticides can have long-term impact on bumblebee learning
Bumblebees fed tainted food as larvae had trouble learning later in life

Bumblebees are important pollinators, and pesticides are putting them at risk.
schnuddel/E+/Getty Images Plus
The soft sound of bees buzzing among flowers signals warm weather throughout the world. But in many places, those sounds are fading. And it’s not just honeybees that are struggling. Native bees, including bumblebees, are also becoming scarce. Factors such as climate change and habitat loss may be partly to blame. But a new study points to the threat posed by a common pesticide. Bumblebees exposed to this chemical had a harder time learning. And it was true even when bees ate pesticide-laced food only as larvae.
That’s a concern because affected bees could have a harder time finding food.
Bumblebees make up about 250 of the world’s 20,000 bee species. Most native bees go it alone. But the bumbles are social. They live in colonies of 50 to several hundred bees, depending on the species. Like honeybee workers, bumblebee workers collect pollen and nectar. Then they bring it back to the nest to feed the young. Anything interfering with this process could pose threats to the colony.
And threatened they are. Nearly one in three species of bumblebee is becoming harder to find. That’s a big concern — for everyone. Bumblebees are important pollinators for all types of plants. They vibrate their bodies against flowers. This releases pollen that most other bees can’t access. That makes them essential for a variety of flowering plants, including tomatoes. If you like pizza or spaghetti, you need bumblebees!
The problem with pesticides
People use pesticides to control insects, including ones that damage plants. But such chemicals can harm animals other than their intended targets. Research has found that insect pollinators, such as bees, are especially vulnerable. Because these insects travel from flower to flower, they are exposed to pesticides again and again. Bees often take pesticide-laced nectar and pollen back to their nests. This can expose every bee in the nest, even larvae.
Bee colonies grow over time, as new bees hatch. Researchers have tested the effects of pesticides on colony size. Such studies found that colony growth slows after pesticide exposure. But curiously, those effects did not show up for several weeks.
These findings got Richard Gill wondering what, exactly, was going on. Gill is an insect ecologist in England at Imperial College London. Was the pesticide affecting larvae? If so, any impacts might have had to wait until those larvae grew into adults.
To find out, Gill and his team studied 22 bumblebee colonies. This included a total of 413 bees. The researchers assigned each colony to one of four treatments. Five colonies served as controls. They received pollen and a sugar water solution, but no pesticide. The other three groups received sugar water laced with imidacloprid (Ih-mid-uh-CLOH-prid). This pesticide is used around the world to control sucking and chewing pests. (These include aphids, thrips, whiteflies and some beetles.) The researchers added only a tiny amount to the sugar water. This was roughly equal to what the bees encounter when foraging on plants treated with this chemical.
Six colonies received the pesticide only during the study’s first three weeks. That’s how long it takes for a larva to become a pupa and then emerge as an adult. Another six colonies received the pesticide from day 22 to the end of the study, around day 45. The bees here were exposed only as adults. The remaining five colonies received the pesticide-laced water throughout the study.
Gill and his team then tested the ability of three- and 12-day-old bees to learn. They harnessed each one and placed it in front of a gently blowing fan. The fan blew lemon-scented air at the bee for 10 seconds. Halfway through this time, the researchers touched the bee’s antenna with a drop of sugar water. This caused the bee to stick out its tongue-like proboscis (Pro-BAA-sis). They then let the bee drink the sweet treat.
Healthy bees use scent to help them find flowers. The lemon scent mimicked a bee’s natural process of detecting an odor and getting a nectar reward. After 10 minutes, the researchers gave each bee the same lemony scent followed by sugar water. They repeated their process 10 times for each bee.
After the learning experiment, the team scanned each bee with a micro-CT scanner. This tool created a 3-D image of structures in its brain. The team focused on structures called mushroom bodies. (When viewed from the side, they look like mushrooms.) These regions are where insects process information and form memories.
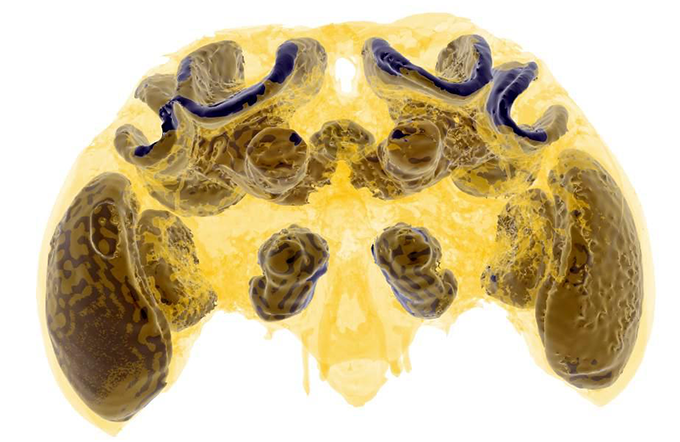
Damaged brains
Gill’s team found that bees not exposed to the pesticide learned quickly. Some needed just two or three tries before sticking out their proboscis when they smelled lemon. (Much like you might salivate at the smell of baking cookies.) Bees exposed to the pesticide — in all three treatment groups — struggled to link that scent with the reward. They took longer to respond to the lemony odor. Some never did.
Older bees (12 days old) learned faster than younger bees. Critically, exposure to pesticide during the first three days of adult life seemed to cause the most problems. “Bee brains are still undergoing a lot of change, making it a vulnerable period in their life,” Gill explains.
On average, bees exposed to pesticide had smaller mushroom bodies than did those in the control group. There was variation in size, though. Among control bees, those with larger mushroom bodies learned faster. That wasn’t true among the pesticide groups. Having bigger mushroom bodies didn’t make it easier for those bees to learn.
Educators and Parents, Sign Up for The Cheat Sheet
Weekly updates to help you use Science News Explores in the learning environment
Thank you for signing up!
There was a problem signing you up.
“Mushroom bodies are mostly responsible for learning and cognition,” Gill explains. Pesticide exposure during early life “may have affected the development of the neurons inside the mushroom body,” he says. This results in a kind of brain damage. “The bee did not have the nerve network it needed to perform the simple task.”
The team published its findings online March 4 in Proceedings of the Royal Society B.
The study highlights the risk of imidacloprid and other, similar pesticides to all stages of bumblebee colonies, says Elaine Evans. She is a bumblebee researcher at the University of Minnesota in St. Paul. That risk extends from “solitary queens founding nests, to fully developed colonies with workers, males and queens,” she notes. However, she cautions, not all bees exposed to pesticide get a dose as large as the ones in this study. And that makes it difficult to know the real-world impacts of these pesticides on bumblebees, she says.
It’s essential to consider the broader effects of pesticides before using them, Gill says. “If colonies are exposed to [toxic chemicals], then the baby bees developing inside can be at risk.” That can have a serious impact on the entire colony. If a colony is producing impaired workers, it can’t function well. And that puts it at risk of collapsing, he says.
How, then, can growers prevent insect damage to their gardens and crops? One solution: Plant a variety of native plants. These attract pests’ natural predators. That can keep pests in check and limit damage, without unintended harm to pollinators.







