How math makes movies like Doctor Strange so otherworldly
Patterns called fractals are inspiring filmmakers with ideas for mind-bending worlds

Kaecilius, on the right, is a villain and sorcerer in Doctor Strange. He can twist and manipulate the fabric of reality. The film’s visual-effects artists used mathematical patterns, called fractals, illustrate Kaecilius’s abilities on the big screen.
Marvel Studios
For wild chase scenes, it’s hard to beat Doctor Strange. In this 2016 film, the fictional doctor-turned-sorcerer has to stop villains who want to destroy reality. To further complicate matters, the evildoers have unusual powers of their own.
“The bad guys in the film have the power to reshape the world around them,” explains Alexis Wajsbrot. He’s a film director who lives in Paris, France. But for Doctor Strange, Wajsbrot instead served as the film’s visual-effects artist.
Those bad guys make ordinary objects move and change forms. Bringing this to the big screen makes for chases that are spectacular to watch. City blocks and streets appear and disappear around the fighting foes. Adversaries clash in what’s called the “mirror dimension” — a place where the laws of nature don’t apply. Forget gravity: Skyscrapers twist and then split. Waves ripple across walls, knocking people sideways and up. At times, multiple copies of the entire city seem to appear at once, but at different sizes. And sometimes they’re upside down or overlapping.
Bringing the twisty other world of Doctor Strange to the big screen required time, effort and computers. Wajsbrot also needed a geometric pattern called the Mandelbrot (MAN-del-broat) Set. This is a type of shape known as a fractal. It’s made of curves and patterns, but those curves and patterns have curves and patterns of their own. There are patterns within patterns. And similar ones show up as you zoom in on an object. This happens in nature, too. Zoom in on a jagged mountain top and you find smaller jagged peaks within the peaks.

The people who worked on special effects for Doctor Strange wanted to use a lot of fractals, says Wajsbrot, who works with a company called Framestore. As characters try to navigate bizarre changes to their reality, scenes zoom in or out on a building, wall or floor. And this reveals more buildings, walls and floors within. The filmmakers’ goal was to use math to create sights that people had never seen in a movie before. To get that type of novelty, Wajsbrot says, they needed fractals. And of all the fractals they worked with, they found special inspiration in one type — the Mandelbrot Set.
“The Mandelbrot Set,” says Wajsbrot, “was the cherry on the cake.”
Monsters, infinities and snowflakes
The Mandelbrot Set is named for Benoit B. Mandelbrot. He was a Polish-born mathematician who studied math in Paris, France. He would go on to spend most of his life in the United States working for IBM, the computer company. He died in 2010. Mandelbrot is most famous for his studies of fractals. (In 1975, he even coined the term fractal to describe these shapes.)
Mandelbrot didn’t invent or discover these shapes. Earlier mathematicians had explored them. In 1904, for example, a Swedish mathematician named Niels Fabian Helge von Koch (Fon KOKH) devised one of the most famous fractals in history.
Von Koch’s fractal is a little easier to grasp than the Mandelbrot Set. Here’s his recipe: Start with an equilateral triangle (that’s one where each side is the same length). Then remove the middle third of each side. Now, build an equilateral triangle in each of those places where you removed the line. Keep going: Everywhere you find a line segment, remove the middle third and build an equilateral triangle there.
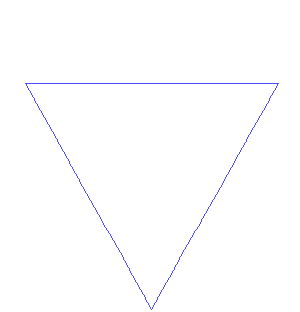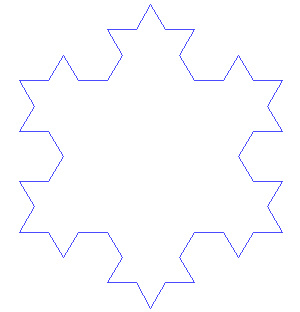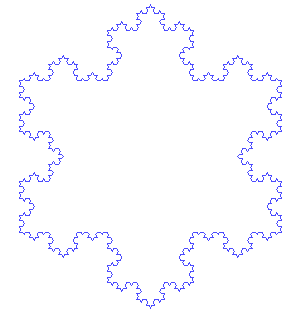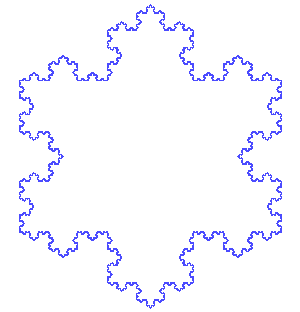
The figure is known as von Koch’s snowflake. Mathematicians called shapes like this “pathological curves.” (“Pathological” things cause, or are caused by, physical or mental disease.) They sometimes called them mathematical “monsters” because the shapes don’t follow easy rules. For example: If you keep going with von Koch’s process forever, you’ll end up with an infinitely long line. Von Koch’s snowflake is a fractal. If you zoom in on it, anywhere, you’ll find the same pattern of triangles on triangles.
One of Mandelbrot’s early demonstrations of a fractal was similar to von Koch’s snowflake. It arose from a question: How long is the coastline of Great Britain? The question seems simple. The answer isn’t.
Measure a coastline on a globe or from satellite images, and you can use a ruler to find the solution. But if you hop in a boat and follow the rocky coastline all the way around, you’ll get a larger number. (That’s because you can measure more twists and turns, which add distance.) If you walk the whole length, you’ll get a still bigger number.
If you could enlist a crab to do the measurement for you, its report would be even bigger. That’s because it would have to scramble over or around every rock it encountered.
Mandelbrot showed that the measured length depends on the size of your ruler. The smaller your ruler, the larger your answer. By that process, he said, the coastline is infinitely long.
Nature is truly rough
Geometry — the math of curves and other shapes — involves straight lines and neat circles. Mandelbrot argued that those concepts don’t describe the roughness of the natural world. Many objects in nature, including mountains, clouds and coastlines, look the same from far away as they do up close. In order to study these irregular shapes better, Mandelbrot turned to the idea of dimension.
A line has one dimension. (The lines making up the letters of this article, for example, are one-dimensional.) A plane, like a sheet of paper, has two dimensions. A box has three. But Mandelbrot’s idea was that rough, natural shapes, such as coastlines or clouds, have a dimension somewhere between two whole numbers. He said they have a fractional dimension, which inspired him to make up the term “fractal.”
Mandelbrot’s work opened a new area of math exploration, starting in the 1970s and 1980s. For artists, it led to new ways of creating landscapes. Mandelbrot showed that math could be used to create a realistic scene of mountains, water, clouds or other things in nature. The equations that make fractals soon became tools for artists.

“A lot of people may not even realize they are looking at a fractal design that was created with math,” says Hal Tenny. This New Jersey artist creates his art using fractals. “With the different computer programs we have now, we can create almost photorealistic fractal images that are so different than what we are used to seeing with ordinary images.”
The Mandelbrot set grows up — and out
The Mandelbrot Set might be the most famous fractal of all. Like the von Koch snowflake, the Mandelbrot Set follows a mathematical recipe that tells you to repeat the same steps over and over and over. Mathematicians call this an iterative process.
The basic recipe for a Mandelbrot Set includes only multiplication and addition. These are done over and over, again and again. “It is this amazing thing that comes from such a simple rule,” says Sarah Koch. A mathematician, she works at the University of Michigan in Ann Arbor. Koch is an expert in a field called complex dynamics.
Her work often leads her back to the Mandelbrot Set. It looks like a bug with lots of smaller bugs around its edges. Zoom in on those exterior bugs, and still smaller bugs, identical in shape, appear. (Other patterns, with names such as Seahorse Valley, also appear.)

Mathematicians still don’t know everything about the ultimate outermost edge of the Mandelbrot Set. It’s not a neat line or curve. It’s so twisty that the further you zoom in, the more twists you discover. There are other shapes lurking near the edge, too.
“If you take a Mandelbrot Set and zoom in anywhere around the boundary, you will find a baby Mandelbrot Set that’s close to the place where you’re zooming in,” Koch says. “The Mandelbrot Set has small copies of itself inside of itself.”
One of the most surprising things is that the Mandelbrot Set pops up even when people aren’t looking for it. Mathematicians have created graphs that should have nothing to do with the fractal. Yet when they zoom in on the pattern, they discover tiny copies of the Mandelbrot Set.
“It’s everywhere when you start to iterate,” says Koch. It’s so common, she says, that mathematicians now recognize the Mandelbrot Set as something basic, like an element in chemistry. It’s a building block of other shapes. “It is one of the fundamental objects in the field.”
Perhaps that’s the reason it’s been so irresistible to mathematicians and computer programmers alike. As computers became more popular in the 1980s and 1990s, people began writing code to show the Mandelbrot Set and other fractals on screens.
Soon they began to wonder: What would a three-dimensional version of the Mandelbrot Set look like?
Many programmers have now developed mind-bending spaces based on it. One of those is Tenny, who says he “works on fractals daily,” incorporating them into his art.
His digital images look like bizarre worlds that are both familiar and unbelievable at the same time. They’re so convincingly alien that, a few years ago, he heard from people working on a new movie about aliens. It was called Guardians of the Galaxy, Vol. 2.
From ‘Mandelbulb’ to movie star
The Guardians filmmakers asked Tenny to send in his ideas about what exotic, faraway planets might look like. Part of the 2017 movie takes place on a planet inhabited by Ego, a conceited and powerful creature with bad plans for the universe. That’s where Tenny saw his ideas on the big screen.
“Parts of my images had been selected and composited together by other artists,” he says. There, in the background, he saw glimpses of a Mandelbulb go flashing by.
What’s a Mandelbulb?
Back in 2007, mathematician Rudy Rucker began writing equations aimed at creating a three-dimensional Mandelbrot Set. He was also a California-based science-fiction writer. His work inspired other computer programmers to work on the project. One of them, Daniel White, gave the project a name: the Mandelbulb.
Paul Nylander was another one of those programmers. Now a mechanical engineer in Los Angeles, Calif., he first learned about the Mandelbrot Set in 2001. At the time, he was in college. “I asked the professors . . . in the math department what they knew about it,” he recalls. After lots of trial and error, he managed to write his own Mandelbrot computer program. “I finally figured out how to do it.”
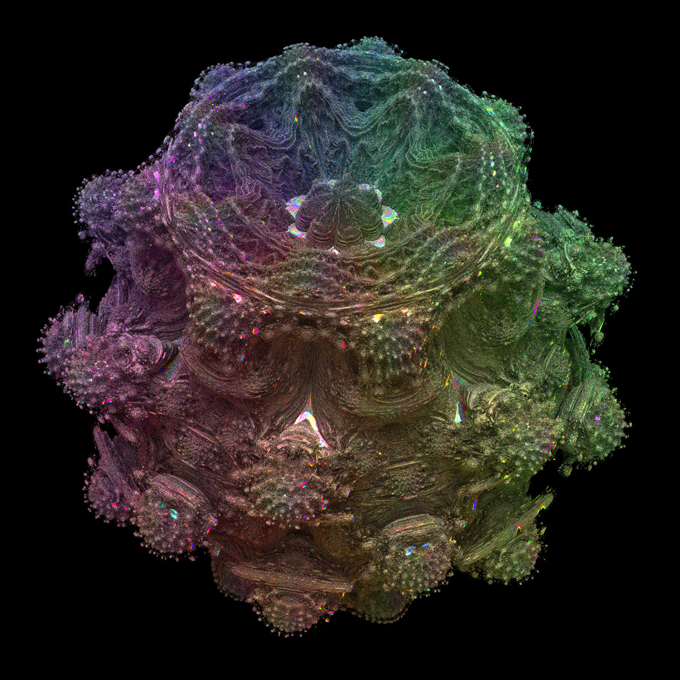
Eight years later, he found an online discussion about creating three-dimensional fractals. He read about the work of Rucker and other programmers. After 10 days, he produced an image of a 3D Mandelbrot Set that he liked. He posted the blob-like Mandelbulb image to the online group. Since then, the Mandelbulb has taken on a life of its own.
After seeing the 2017 Guardians of the Galaxy sequel, Tenny recalls being told “that some of my designs were pivotal in the direction they eventually took for Ego’s palace and other areas.”
Nylander says he’s seen many recent movies that draw inspiration for special effects from the Mandelbulb. At the end of the 2014 animated flick, Big Hero 6, the main character tries to rescue his robot from a strange otherworld filled with floating, Mandelbulb-like shapes. In the 2018 science fiction movie Annihilation, a translucent, jelly-like wall streams with Mandelbulbs. The alien in that movie, too, seems to be made from that shape.
Beyond the Mandelbulb
And then, of course, there’s Doctor Strange. “We are quite fond of fractals,” says Wajsbrot. “Quite early on we knew we wanted to use Mandelbrot.”
But they didn’t use the Mandelbulb. Instead, they tested a shape called the Mandelbox. It’s a cube that looks like it’s engraved or carved into Mandelbrot-like patterns. The Doctor Strange team ended up using a similar shape, called the Mandelsponge, which is also a fractal. To control the fractal — and create the illusion of worlds within worlds — the filmmakers had to use powerful computer programs.
Getting the look just right took more than a year. “On Doctor Strange, the Mandelbrot is one of the first effects we tried to nail,” Wajsbrot says. “And it was the last we delivered.”
Wajsbrot also worked on fractal images for Guardians of the Galaxy Vol. 2. More recently, his group used the math shapes to model undersea corals in the 2018 Mary Poppins Returns. They’ve also created a virtual-reality program called CORAL, based on fractal patterns. It’s an immersive world, full of self-similar shapes.
“It is aimed at discovery and exploration, giving the user infinite space to discover the beauty of mathematics,” says Wajsbrot. Looking for beauty and wonder, he says, is an important part of his job. “A good visual-effects artist needs to be open-minded and curious about the world he lives in. And there are so many interesting things in fractals.”







